역전파 알고리즘의 생물학적 타당성

현재 인공신경망의 주류 학습 알고리즘은 오류 역전파 (backprop) 방식에 의존하고 있다. 해당 알고리즘의 성능이 탁월하다는 것은 다양한 분야에서 이미 입증되었다.

 

인공신경망은 뇌의 뉴런들의 연결 구조에서 영감을 받아 만든 구조이다. 즉 bio-inspired하다. 그런데 이 bio-inspired한 구조를 학습하는 주류 방법인 backprop 방법은 bio-inspired가 아니다. 하지만 bio-inspired가 아니어도 biologically plausible(생물학적으로 설명 가능)할 수도 있다. 과연 이 backprop 방법이 biologically plausible할까? 즉 실제 우리 뇌에서 실현이 가능할까? 결론은 간접적으로 타당하다. 한번 살펴보도록 하자.

 

본 글에서는 feedback alignment와 predictive coding paradigm을 중심으로 설명하겠다.

 

Backprop

간단한 MLP 구조를 예시로 backprop을 상기시켜보자.

한 개의 은닉층을 가지는 MLP

위 MLP의 θ는 MLP의 연결 가중치 집합이다. θ는 학습 전에 랜덤하게 초기화된다. 간단한 예시이므로 데이터 한 개만을 가져왔다(벡터 X, Y 한 쌍). 이 MLP의 목적은 X를 넣으면 Y가 나오도록 θ를 조정하는 것이다. 어떻게? backprop으로.

 

이름이 backprop(역전파)인 이유는 먼저 forwardprop(순전파)이 있어야 하기 때문이다. 초기화된 가중치 집합 θ를 이용해서 먼저 forwardprop을 해보자.

 

순전파(forwardprop)

X를 집어넣었더니 Ŷ이 나왔다. 이 MLP는 방금 X에 대한 결과가 Ŷ라고 대답했다. 이렇게 forwardprop은 끝났다.

 

이 MLP는 지금 틀렸다. X에 대한 결과는 Ŷ가 아니라 Y기 때문이다. 얼마나 틀렸는가? |Y-Ŷ| 만큼 틀렸다. 여기서 |Y-Ŷ|를 오차함수 E(Ŷ)라고 표현해보자. E(Ŷ) = 0이라면 이 MLP는 정답을 완벽하게 맞춘 셈이다. 아무리 잘 해도 딱 0보다는 조금 더 크겠지만, 어찌되었든 오차는 최소일 수록  잘 맞춘 것이다. 그런데 여기서 한 가지 더. Ŷ는 X와 가중치 집합 θ에 의해 계산된 값이다. X랑 Y는 데이터이므로 고정된 값이고, θ가 지금 우리가 조정해야 하는 값이다. 그러니까 오차 E(Ŷ)는 결국 가중치 집합 θ에 의한 함수 E(θ)이다. 즉 이 MLP가 정답을 맞추게끔 하려면 E(θ)가 최소가 되게끔 하는 θ를 찾으면 된다.

 

어떤 함수 f(x)의 값이 최솟값이 되게 하는 x을 구하려면 경사를 타고 내려가보면 된다는 것이 경사하강법의 아이디어다.

그럼 함수 E(θ)의 값이 최솟값이 되게 하는 θ를 구하기 위해 경사를 타고 내려가보면 된다.

 

오차를 최소화하기 위해, 오차에 미치는 가중치의 경사가 하강하는 방향으로 가중치가 갱신된다.

초기 가중치 집합을 θ1이라고 하자. θ1에서의 경사는 위에서 보이듯이 E를 θ1로 미분한 값이다. 저 경사값을 이용해서 오른쪽의 식과 같이 θ1를 θ2로 업데이트한다. η는 학습률 상수이다. 이렇게 한 번 업데이트하는 데에 forwardprop과 backprop을 한 번씩 한다. 이 θ 업데이트 과정이 바로 학습이다. 이 학습을 계속 반복해서 θ를 계속 업데이트하다보면 E가 최소인 지점 θ*로 도달할 것으로 기대할 수 있다. 이것이 경사하강법이다.

 

근데 이 글에서 중요한건 backprop이다. θ1를 θ2로 업데이트할 때, dE/dθ1은 무엇을 의미하는가? 바로 MLP의 가중치 집합 θ1이 오차 E(θ1)에 미친 영향도를 의미한다. 이것을 기준으로 가중치 집합은 업데이트될 수 있다.

오차에 각 가중치가 미치는 영향(편미분값)으로 가중치를 업데이트한다. 모든 편미분 값은 출력층으로부터의 편미분값에 연쇄 법칙을 역방향으로(입력층까지의 방향으로) 적용해가며 구할 수 있다. 

θ는 여러 가중치들을 뭉쳐서 표현한 것이다. 우리가 θ를 업데이트한다는 것은 사실은 이 MLP의 연결 가중치 하나하나를 개별적으로 업데이트한다는 것을 의미한다. 위 그림과 같이 첫번째 층의 첫번째 뉴런의 첫번째 연결 가중치를 w(1)11 라고 했을 때, 이 가중치를 업데이트 하는 식은 위의 빨간 네모박스와 같다. 이걸 모든 가중치들에게 일괄 적용한다. 결국 θ를 업데이트하기 위해서는 오차 E를 각각의 가중치에 대해서 편미분한 값 σE/σw을 구해야 한다.

 

연쇄 법칙의 적용

2개의 층으로 이루어진 위 그림의 MLP를 예로 든다면, 1번째 층의 σE/σw 값을 구해내기 위해서는 먼저 2번째 층(출력층)의 σE/σw를 구해야 한다. 이 2번째 층은 오차 E와 가장 밀접한 층이므로 직접 구할 수 있다. 2번째 층의 σE/σw가 일단 구해지면, 1번째 층의 σE/σw는 연쇄법칙(chain rule)을 이용해서 구해낼 수 있다. 이렇게 가중치에 대한 경사를 전파하는 과정이 마지막 층에서부터 점차 이전 층으로, 즉 역순으로 연쇄법칙에 따라 전파되기 때문에 역전파(backpropagation)로 명명되었다.

 

Backprop, 생물학적으로 타당하지 않다?

Backprop은 알고리즘적으로는 뛰어나지만, 뇌/인지/신경과학으로부터 생물학적으로 타당하지 않다는 지적을 받는다. 어떤 점에서 그럴까?

 

1. 실제 신경망에서, 단일 뉴런의 자극 전달 방향은 단방향이다.
2. 실제 신경망에서, (n+1)층에서 n층으로 향하는 feedback 시냅스 연결 가중치가 forwardprop 시의 (n+1)층 시냅스 연결 가중치와 일치할 리가 없다.
3. 실제 신경망은 인접 뉴런들 간의 local한 연결로 이루어진 병렬적인 구조이다. 이런 구조에서는 MLP처럼 출력층에서 발생한 오차 정보를 인접하지 않은 층으로 global하게 전달하는 것이 불가능하다.

당장은 무슨 이야긴지 와닿지 않을 수 있다. 1번부터 차례로 풀어 설명해보겠다.

 

실제 뉴런(왼쪽)과 인공 뉴런(오른쪽). 실제 두 뉴런을 연결하는 시냅스는 물리적으로 단방향으로만 신호 전달이 가능하다. 그러나 인공 신경망에서 의 시냅스는 추상적인 개념으로 양방향 전달이 가능하다.

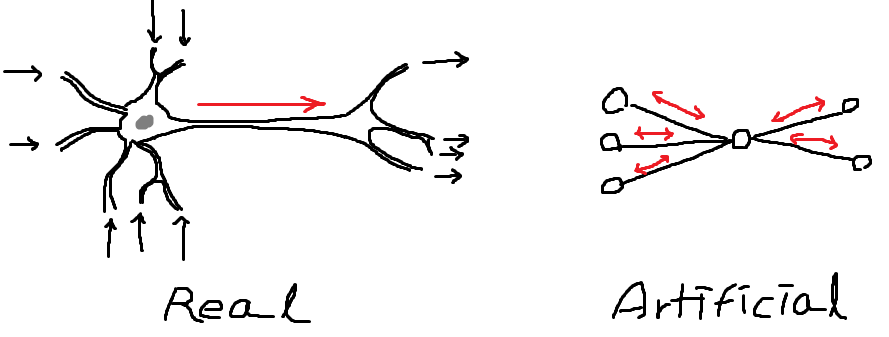
1번의 경우는 가장 기본적인 신경 세포 구조상의 문제로, 실제 뉴런과 연결된 시냅스는 신호 전달 방향이 한 방향으로만 흐르기 때문에 backprop처럼 양방향 통신이 불가능하다는 것이다. 그렇다면 아예 feedback 자체가 불가능한 것일까? 그렇지 않다. 단일 뉴런의 자극 전달 방향이 단방향이라는 것이 다시 자극이 돌아오는 경로가 없다는 것을 의미하지는 않는다. 실제로, 뉴런들의 연결 구조에서 feedback이 가능한 경로가 많이 발견되었다. 이를 reciprocal connection이라 한다. (아래 그림)

축색을 통해 전달했던 신호가 다시 수상돌기로 입력될 수 있는 경로인 reciprocal connection은 feedback의 가능성을 열어 둔다.

reciprocal connection의 존재는 feedback을 가능하게 한다. 따라서 뇌가 이 feedback 통로를 이용해 backprop을 할 수도 있다는 가능성은 열려 있다. 하지만 여전히 실제 뇌에서 backprop의 실현가능성은 많은 문제가 남아있다.

 

그 중 하나가 'weight transport problem'이라고 불리는 2번과 같은 문제이다. backprop 알고리즘에서는 n층의 forwardprop 경로 가중치를 갱신하기 위해 (n+1)층의 forwardprop 시에 사용되었던 연결 가중치 정보를 필요로 한다. 따라서 (n+1) 층에서 n층으로 향하는 feedback 경로의 가중치는 (n+1)층의 가중치와 정확히 일치해야 하는데(weight symmetry 조건이라 한다), 실제 뇌에서는 도저히 이런 정교한 작업이 실현될 수가 없다는 것이다. (아래 그림) 심지어 매 forwardprop, backprop마다 forwardprop 경로의 가중치가 갱신될 텐데 과연 실제 신경망에서 n층으로 향하는 feedback 경로의 가중치가 매 순간 (n+1)층에서의 forwardprop 경로의 가중치와 정확히 대칭일 수가 있을까? 불가능에 가깝다.

 

backprop에서의 weight symmetry 조건. 이 조건 달성의 어려움에 의해 weight transport problem이 제기되었다.

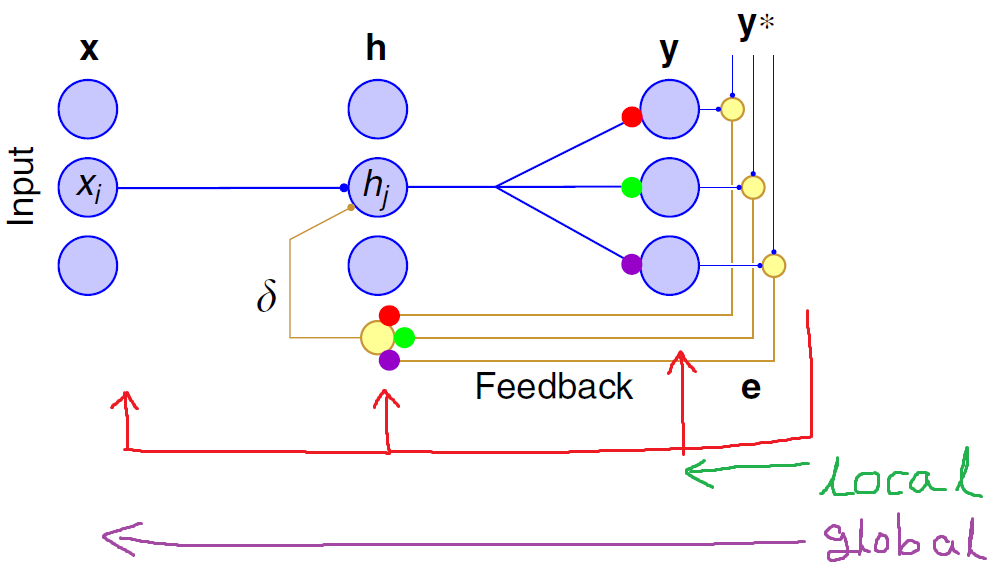
또 하나의 문제는 실제 뇌에서 오차가 global하게 전달될 수 없다는 3번과 같은 문제이다. MLP의 backprop에서는 출력층에서 발생한 오차를 역으로 전파하여 멀리 떨어져 있는 입력층까지 오차를 전달하는데(이를 global한 전달이라 한다), 실제 뇌에서는 인접한 뉴런들 간의 feedback 경로는 인정해도(이는 local한 전달이라 한다) 오차 발생 지점으로부터 멀리 떨어져 있는 뉴런들까지 feedback 경로가 정교하게 구성되어 있을 수 없다는 것이다. (아래 그림)

 

인접한 뉴런들 간의 local한 연결을 통한 오차의 전달은 생물학적으로 어려운 일이 아니다. 하지만 인접한 뉴런을 넘어 멀리에 있는 뉴런까지 오차를 전달하는 것이 과연 실제 신경망에서 일어날 수 있을까? 신경과학자들은 실제 신경망에서 이러한 global한 경로의 통제는 어려운 일이라고 이야기한다.

분명 backprop에 필요한 이러한 제약조건들은 실제 뇌에서 도저히 실현될 수가 없는 것들이다. 따라서 backprop은 생물학적으로 실현 불가능하다. 하지만 어쩌면 backprop에 필요한 제약조건들이 너무 강력했던 것이 아닐까? 만약 이 제약조건들이 조금 느슨해져도 backprop과 같은 학습효과를 낼 수 있다면? 즉, 뇌에서 실현 가능한 어떠한 'backprop에 근사하는 방법'이 존재한다면 backprop은 간접적이지만 생물학적으로 타당하다고 할 수 있지 않을까?

 

우선 reciprocal connection의 존재로 인해 1번의 문제는 해결되었다. 다음 두 절에서는 backprop의 생물학적 타당성을 뒷받침하는 feedback alignment 이론 및 predictive coding 패러다임을 소개한다. feedback alignment는 2번의 문제를, predictive coding 패러다임은 3번의 문제를 해소한다.

 

Feedback Alignment

Timothy P. Lillicrap의 Random synaptic feedback weights support error backpropagation for deep learning (2016)에서 제시하는 feedback alignment라는 개념은 backprop의 생물학적 타당성을 뒷받침하는 이론 중 하나다.

 

해당 논문은 2번에서 제기되는 weight transport problem 문제를 해소한다고 주장한다. weight transport problem이란 무엇이었는가? n층으로 향하는 feedback 경로의 가중치가 (n+1)층의 forwardprop 경로의 가중치와 정확히 대칭이어야 하는 조건(weight symmetry 조건)을 의미했다. 하지만 사실 그렇게 강력한 조건이 필요가 없다고 해당 논문에서는 이야기한다. feedback 경로의 가중치를 고정된 아무 랜덤 값으로 바꿔도 딱 하나의 약한 제약조건만 만족한다면, backprop과 유의미한 성능의 차이 없이 학습이 이루어진다는 것이다.

 

Feedback alignment을 직역하면 '피드백 정렬'이다. 필자의 의견에 따르면 이 '피드백 정렬'의 의미는 대강 '난잡하게 발생하는 피드백 신호를 정렬하여 용이하게 함'의 뜻이다. 즉, 고정된 랜덤한 feedback 경로의 가중치를 타고 들어오는 feedback 신호를 forwardprop 경로의 가중치가 알아서 적응(정렬)해서 학습에 사용한다는 것이다.

 

한마디로, backprop처럼 정교한 값으로 feedback 해줄 필요 없이 feedback을 대충 해주기만 하면 뉴럴넷이 알아서 그 feedback 신호까지 학습해버린다는 이야기이다.

 

기존 backprop 방법의 weight symmetry 조건(좌)과 feedback alignment 방법에서 랜덤한 값으로 고정된 행렬 B를 이용하여 weight symmetry 조건을 해소한 모습(우)

위 그림을 보자. 왼쪽이 정통 backprop 방법이다. feedback 경로의 가중치 행렬이 forwardprop 경로의 가중치 행렬과 일치해야 하는 제약조건을 볼 수 있다. 그런데 이 feedback 경로의 가중치 행렬를을 오른쪽 그림과 같이 그냥 랜덤한 값으로 고정된 B라는 행렬로 치환해도 학습은 동일하게 이루어진다는 것이다. 신기하지 않은가?

 

이것이 가능한 이유는 backprop의 학습 규칙 자체가 애초에 경험적이고 반복적이라는 데에 있다. 경사하강은 한 번만으로 학습이 되지 않는다. 여러번의 경사하강이 누적되어야 비로소 최소 오류 지점(지역적일 수도 있다)에 도달한다. 즉, 경사하강은 원래 그 하강하는 양보다도 방향이 훨씬 더 중요하다는 것이다. 일단 방향만 맞으면 어쨌든 경사하강에 의해 학습은 이루어진다.

 

W0를 n층의 가중치, h=xW0, W를 (n+1)층의 가중치라 했을 때 기존 backprop에서의 가중치 갱신량 비례식(검정). W0의 가중치 갱신량의 우변에서 -W를 랜덤한 값으로 고정된 행렬 B로 치환하여도 비례식은 유지될 수 있다.

방향에 대한 이야기를 위와 같이 식으로 나타내 볼 수 있다. W0은 n층의 가중치이고, h=xW0이며, W는 (n+1)층의 가중치이다. W0의 가중치 변화량은 아래 식의 우변과 비례한다. 이는 비례식이므로, 방향만 같다면 그 값이 정교할 필요는 없다. 이것이 feedback alignment의 아이디어로, 우변의 -W를 랜덤한 값으로 고정된 행렬 B로 치환하여도 비례식이 유지될 수 있다. 즉, 학습에 큰 영향이 없을 것이라는 것이다. 실제로 논문에서는 MNIST를 이용하여 실험한 결과를 소개하고 있으며, backprop과 유의미한 성능 차이가 없음을 보인다.

 

하지만 이 행렬 B가 딱 하나의 약한 제약조건을 만족해야 한다고 했다. 그것은 방향 조건으로, 값이 정교할 필요는 없어도 방향은 일치해야 올바른 학습(가중치 갱신)이 이루어질 수 있다. 그 조건은 기존 backprop에서 사용하는 feedback 값의 일부인 We와 feedback alignment에서 사용하는 feedback 값의 일부인 Be의 각도 차이 < 90º 이라는 것이다. 결국 W와 B가 유사할 수록 좋다는 것인데, 사실 이것은 무시할 수 있는 조건이다. 왜냐하면, W가 계속해서 갱신되면서 B에 맞추어 alignment 하기 때문이다(이 때문에 저자는 이 방법을 'feedback alignment'라 불렀다). 이 alignment 과정을 통해 각도 차이는 줄어든다. (아래 그림)

 

We와 Be의 각도 차이가 90도 안쪽으로 줄어들며 alignment된다(좌). 각도 차이가 0에 수렴하지 않음에도 MSE의 감소폭은 backprop과 feedback alignment에서 거의 유사하다(우).

위 그림의 왼쪽 그래프를 보면 We와 Be의 각도 차이는 학습을 거듭하며 90도 안쪽으로 줄어들어 alignment된다. 우측 그래프는 backprop과 feedback alignment의 손실(MSE) 감소폭을 보여주는 그래프이다. 중요한 것은, alignment가 0도까지 수렴하지 않았는데도 (0도에 수렴하면 backprop과 feedback alignment은 같아진다) MSE의 감소폭에 유의미한 차이가 없었다는 것이다. 이는 backprop에서 요구하는 weight symmetry 조건은 학습을 위해 너무 과한 조건임을 시사한다.

 

Feedback alignment에 의하면 결국 feedback 경로만 있다면 그 가중치는 어떤 값이 되든 상관이 없어진 셈이다. 다른 건 몰라도, 이 정도라면 실제 신경망에서 backprop을 구현하기에 훨씬 쉬워진 것이 아닌가?

 

다만, feedback alignment에서는 출력층에서 발생한 오류값 e가 global하게 전달되고 있다고 가정하고 있다. 이 가정 역시 실제 신경망에게는 상당한 제약조건이다. 다음 절에서는 이 오류 전달의 global 조건을 해소하고자 하는 면에서의 predictive coding 패러다임을 살펴보겠다.

 

Predictive Coding

Predictive coding paradigm이란, 우리 뇌가 주로 미래에 입력될 감각을 예측하는 일을 한다는 이론이다.

 

현재 시각이 t일때의 감각을 받아 시각이 t+k일 때(미래)의 감각을 예측한다.

위의 날아가는 야구공을 현재의 감각 입력이라고 했을 때, 뇌에서는 미래의 감각 입력을 미리 예측하고, 또 예측이 가능하도록 학습한다는 것이다. 이러한 예측이 가능하면 우리는 행동을 계획(planning)할 수 있다.

 

Predictive coding paradigm은 이론 그 자체로도 생물학적 타당성을 지니고 있다. 학습을 위한 '정답' 데이터가 감각을 통해 직접 입력되기 때문이다.

 

실제로 k만큼 시간이 지나 현재 시각이 t+k일 때의 감각을 받아 예측했던 값과의 오차를 얻어 학습한다.

위의 그림처럼, 예측하는 것은 미래의 감각이기 때문에 실제로 시간이 흘러 미래가 되었을 때 입력받는 감각과 이전에 예측했던 감각을 비교해서 오차를 구할 수 있다. 이렇게 구한 오차로 학습하여 예측을 더 잘 하게 할 수 있다.

 

위의 과정에서 우리의 뇌는 학습에 필요한 정보를 스스로 얻었다. 이는 Predictive coding paradigm의 중요한 속성이다. 인공신경망을 학습하기 위해서는 일종의 '정답'을 제시해주어야 오류를 구하여 그 오류를 통해 backpropagation할 수 있다. 그러나 실제 생물에게는 그러한 종류의 '정답'은 제공되지 않는다. 하지만 Predictive coding paradigm에서만큼은 그러한 '정답'을 감각을 통해 스스로 제공받는다. 이러한 속성은 다른 말로 self-supervised learning이라고도 한다.

 

그렇다면 이제 predictive coding을 신경망 수준에서 적용해보자. James CR Whittington의 An Approximation of the Error Backpropagation Algorithm in a Predictive Coding Network with Local Hebbian Synaptic Plasticity (2017)에서는 인접한 뉴런들끼리 predictive coding 함으로써 backpropagation을 근사하는 방법을 제안하며 심플한 MLP에서 이 방법을 증명한다.

 

이 작업을 확장하여 Beren Millidge의 Predictive Coding Approximates Backprop along Arbitrary Computation Graphs (2020)에서는 MLP뿐만 아니라 CNN, RNN, LSTM 등에서도 인접 뉴런 간의 predictive coding 학습 규칙을 이용하여 효과적으로 backpropagation을 근사할 수 있음을 보인다.

 

자, 그러면 인접 뉴런 간의 predictive coding이라는 건 무엇일까?

 

Backpropagation 방법(위)과 인접 뉴런 간의 predictive coding을 이용한 backpropagation 근사 방법(아래).

위 그림을 보면 위쪽이 기존 backprop 방법이고 아래쪽이 인접 뉴런 간의 predictive coding을 이용하여 backprop을 근사하는 방법이다. Backprop 방법은 오차의 경사 정보를 전달할 때 chain rule에 따라 끝단 뉴런에서 역방향으로 순차적으로 전달한다. 이러한 chain rule은 생물학적 비타당성을 야기한다. 실제 뉴런들은 복수의 뉴런을 거치는 어떠한 전역적인 경로를 관장하여 오차를 전달할 수 없기 때문이다.

 

이제 아래쪽의 predictive coding 방법을 보자. 여기서는 완전히 chain rule을 사용하고 있지 않다. 학습 규칙은 오직 인접한 뉴런들끼리 이루어진다. 예를 들어 뉴런 v1과 v2의 관계를 보자. 뉴런 v1은 predictive coding의 취지에 맞게, 조금 뒤의 미래에 v2의 값이 어떻게 될 것인지 예측한다. 조금 뒤에 v2의 값이 밝혀지면, 오차 ϵ2가 발생한다. 이 오차를 이용하여 v1과 v2의 연결 가중치를 수정할 수 있다. 이때 v1과 v2는 실제로 인접하게 연결되어 있었고 연결 가중치의 수정에 인접한 정보만을 사용하였으므로 생물학적으로 설명하기에 무리가 없다. 이러한 과정을 v0과 v1, v1과 v2, v2와 출력(v3)에서 병렬적으로 진행한다면, 전체 과정이 결국은 backprop의 과정에 근사하게 된다.

 

인접 뉴런들 간의 정보만을 이용해서 전체 오류의 총합(ℱ)에 한 노드가 미치는 영향을 계산해낼 수 있다.

해당 논문에서 실제 구현은 인접 뉴런들의 예측이 가우시안 생성 모델의 모수가 되도록 설정하였다. 자세한 내용은 여기에선 다루지 않겠다. 어찌되었든 인접 뉴런들이 병렬적으로 학습하여 backprop을 근사할 수 있다는 것은, 출력층에서 발생한 오차를 global한 경로를 거쳐 입력층까지 전달할 필요가 없음을 의미한다. 또한, 이러한 병렬적인 학습 알고리즘의 개발은 생물학적 타당성을 위해서 뿐만 아니라 딥러닝의 시간 비용을 줄이는데에 있어서도 매우 중요하다. 연산이 병렬화될 수 있는 부분이 많아질 수록 여러 대의 컴퓨터가 있을 떄 더 짧은 시간 내로 더 높은 효율의 학습이 가능하기 때문이다.

 

Predictive coding은 학습에 시간 개념이 도입된다. 시간 개념이 도입되는 또 다른 생물학적 타당성을 보장하기 위해 시도된 알고리즘은 STDP (spike-timing dependent plasticity) 알고리즘이 있다. 이 글에서는 다루지 않겠으나, 역시 backprop을 STDP로 근사할 수 있음을 보여주는 참조자료(BP-STDP: Approximating Backpropagation using Spike Timing Dependent Plasticity (2018)) 또한 존재한다.

 

생물학적으로 타당한 인공신경망을 향하여

인공신경망의 기본 구조가 실제 뉴런의 모습을 모사했다지만 현재 딥러닝의 동작은 실제 뉴런들이 학습하는 방식과는 아주 상이하다. 뇌의 학습 방식은 대부분이 아직도 풀리지 않은 미스터리로 남아있지만, 가장 뛰어난 지능은 실제 우리의 뇌이기 때문에 이를 더 잘 모사할 수록 더 뛰어난 인공지능 기술이 개발될 것이라고 기대할 수 있겠다.

 

Backpropagation은 비록 생물학적으로 설명이 힘든 부분이 많지만 분명 많은 분야에서 훌륭하게 활약하고 있는 기초 알고리즘이다. 위에서 살펴본 feedback alignment, predictive coding과 같은 방식이 backprop을 근사함을 증명한다면, 디테일한 부분은 인위적으로 대체되었더라도 backprop이 나름 뇌가 학습하는 방식과 많이 닮아있음을 보이는 셈이다.

 

하지만 바로 그 디테일한 부분에서 기존에 있었던 견고한 가정을 허물고 조금 더 유연한, 조금 더 생물학적 매커니즘과 가까운 학습 방식을 연구해나간다면 점차 새로운 시각이 열림과 함께 더 개선된 형태의 학습 알고리즘의 기초 위에서 인류는 더욱 뛰어난 기술적 혜택을 누릴 수 있을 것이다. 다시 말하지만, 결국 인공지능이란 실제 뇌의 동작 수준과 유사하도록 만드는 것이 우리의 이상적인 목표이기 때문이다.